(출처 : http://jalt.org/test/bro_12.htm)
• Pearson r:
– 연속 변수들 간의 상관계수
– 선형적 관계를 가정
• Spearman's r.
– 서열척도들간의 상관계수
– 연속변수라 하더라도 극단적인 값들이 존재하면 Pearson Correlation 대신 Spearman 상관계수를 사용할 수 있음.
– 계산 방법은 자료의 서열을 정한 다음, 이 서열간의 Pearson 상관계수를 계산하면 됨.
• Phi(φ) coefficient.
– 두 범주 변수들간의 상관계수
– 각 범주 변수를 0과 1로 바꾼 다음, 이 둘 간의 Pearson 상관계수로 계산할 수 있음.
– 이 값은 부호가 의미가 없고, 최소값이 0은 아니다.
• Tetrachoric 상관계수
– 범주들간의 상관계수이나, 범주들이 인위적으로 이분화된 경우에 사용하는 이다.
– 이분화되기 전 원래 변수는 정규분포를 띠고 있다고 가정한다.
• 점이연 상관계수 (Point-biserial correlation)
– 하나가 연속변수이고 다른 하나고 이분변수일 때 사용하는 상관계수
– 이분변수를 0과 1로 코딩한 다음 Peason 상관계수를 계산하면이 상관계수가 된다.
– 검사에서 총점과 문항 (correct/incorrect 혹은 yes/no) 간의 상관계수를 구할 때 자주 사용된다.
– 두 집단의 t-검증과 밀접히 관련되어 있다.
• 이연 상관계수 (Biserial correlation)
– 하나가 연속변수이고 다른 하나고 이분변수일 때 사용하는 상관계수이지만 이분변수가 원래 연속변수인데 이분화한 경우에 상용한다.
– 이는 이분화되지 않았을 때 두 연속변수들간의 상관계수를 추정하는 방식으로 상관이 구해진다.
(출처 : http://qpsy.snu.ac.kr/teaching/multivariate/R_V.pdf)
Biserial correlation |
If the sample is normally distributed (i.e., conditions for the computation of the biserial exist), then to obtain the biserial correlation from the point-biserial for dichotomous data:
Biserial = Point-biserial * f(proportion-correct-value)
Example: Specify PTBISERIAL=Yes and PVALUE=Yes. Display Table 14.
+-------------------------------------------------------------------------------------+
|ENTRY RAW MODEL| INFIT | OUTFIT |PTBSE| P- | |
|NUMBER SCORE COUNT MEASURE S.E. |MNSQ ZSTD|MNSQ ZSTD|CORR.|VALUE| TAP |
|------------------------------------+----------+----------+-----+-----+--------------|
| 8 27 34 -2.35 .54| .59 -1.3| .43 -.2| .65| .77| 1-4-2-3 |
Point-biserial = .65. proportion-correct-value = .77. Then, from the Table below, f(proportion-correct-value) = 1.3861, so Biserial correlation = .65 * 1.39 = 0.90
Here is the Table of proportion-correct-value and f(proportion-correct-value).
p-va f(p-val) p-va f(p-val)
0.99 3.7335 0.01 3.7335
0.98 2.8914 0.02 2.8914
0.97 2.5072 0.03 2.5072
0.96 2.2741 0.04 2.2741
0.95 2.1139 0.05 2.1139
0.94 1.9940 0.06 1.9940
0.93 1.8998 0.07 1.8998
0.92 1.8244 0.08 1.8244
0.91 1.7622 0.09 1.7622
0.90 1.7094 0.10 1.7094
0.89 1.6643 0.11 1.6643
0.88 1.6248 0.12 1.6248
0.87 1.5901 0.13 1.5901
0.86 1.5588 0.14 1.5588
0.85 1.5312 0.15 1.5312
0.84 1.5068 0.16 1.5068
0.83 1.4841 0.17 1.4841
0.82 1.4641 0.18 1.4641
0.81 1.4455 0.19 1.4455
0.80 1.4286 0.20 1.4286
0.79 1.4133 0.21 1.4133
0.78 1.3990 0.22 1.3990
0.77 1.3861 0.23 1.3861
0.76 1.3737 0.24 1.3737
0.75 1.3625 0.25 1.3625
0.74 1.3521 0.26 1.3521
0.73 1.3429 0.27 1.3429
0.72 1.3339 0.28 1.3339
0.71 1.3256 0.29 1.3256
0.70 1.3180 0.30 1.3180
0.69 1.3109 0.31 1.3109
0.68 1.3045 0.32 1.3045
0.67 1.2986 0.33 1.2986
0.66 1.2929 0.34 1.2929
0.65 1.2877 0.35 1.2877
0.64 1.2831 0.36 1.2831
0.63 1.2786 0.37 1.2786
0.62 1.2746 0.38 1.2746
0.61 1.2712 0.39 1.2712
0.60 1.2682 0.40 1.2682
0.59 1.2650 0.41 1.2650
0.58 1.2626 0.42 1.2626
0.57 1.2604 0.43 1.2604
0.56 1.2586 0.44 1.2586
0.55 1.2569 0.45 1.2569
0.54 1.2557 0.46 1.2557
0.53 1.2546 0.47 1.2546
0.52 1.2540 0.48 1.2540
0.51 1.2535 0.49 1.2535
0.50 1.2534 0.50 1.2534
To obtain the biserial correlation from a point-biserial correlation, multiply the point-biserial correlation by SQRT(proportion-correct-value*(1-proportion-correct-value)) divided by the normal curve ordinate at the point where the normal curve is split in the same proportions.
There is no direct relationship between the point-polyserial correlation and the polyserial correlation.
(출처 : http://www.winsteps.com/winman/biserial.htm)
Applied Statistics - Lesson 13
More Correlation Coefficients
Lesson Overview
- Why so many Correlation Coefficients
- Point Biserial Coefficient
- Phi Coefficient
- Measures of Association: C, V, Lambda
- Biserial Correlation Coefficient
- Tetrachoric Correlation Coefficient
- Rank-Biserial Correlation Coefficient
- Coefficient of Nonlinear Relationship (eta)
- Homework
Why so many Correlation Coefficients
We introduced in lesson 5 the Pearson product moment correlation coefficient and the Spearman rho correlation coefficient. There are more. Remember that the Pearson product moment correlation coefficient required quantitative (interval or ratio) data for both x and y whereas the Spearman rho correlation coefficient applied to ranked (ordinal) data for both x and y. You should review levels of measurement in lesson 1 before we continue. It is often the case that the data variables are not at the same level of measurement, or that the data might instead of being quantitative be catagorical (nominal or ordinal). In addition to correlation coefficients based on the product moment and thus related to the Pearson product moment correlation coefficient, there are coefficients which are instead measures of association which are also in common use.For the purposes of correlation coefficients we can generally lump the interval and ratio scales together as just quantitative. In addition, the regression of x on y is closely related to the regression of y on x, and the same coefficient applies. We list below in a table the common choices which we will then discuss in turn.
| Variable Y\X | Quantitiative X | Ordinal X | Nominal X |
|---|---|---|---|
| Quantitative Y | Pearson r | Biserial rb | Point Biserial rpb |
| Ordinal Y | Biserial rb | Spearman rho/Tetrachoric rtet | Rank Biserial rrb |
| Nominal Y | Point Biserial rpb | Rank Bisereal rrb | Phi, L, C, Lambda |
Before we go on we need to clarify different types of nominal data. Specifically, nominal data with two possible outcomes are call dichotomous.
Point-Biserial
The point-biserial correlation coefficient, referred to as rpb, is a special case of Pearson in which one variable is quantitative and the other variable is dichotomous and nominal. The calculations simplify since typically the values 1 (presence) and 0 (absence) are used for the dichotomous variable. This simplification is sometimes expressed as follows: rpb = (Y1 - Y0) • sqrt(pq) /Phi Coefficient
If both variables instead are nominal and dichotomous, the Pearson simplifies even further. First, perhaps, we need to introduce contingency tables. A contingency table is a two dimensional table containing frequencies by catagory. For this situation it will be two by two since each variable can only take on two values, but each dimension will exceed two when the associated variable is not dichotomous. In addition, column and row headings and totals are frequently appended so that the contingency table ends up being n + 2 by m + 2, where n and m are the number of values each variable can take on. The label and total row and column typically are outside the gridded portion of the table, however.As an example, consider the following data organized by gender and employee classification (faculty/staff). (htm doesn't provide the facility to grid only the table's interior).
| Class.\Gender | Female (0) | Male (1) | Totals |
|---|---|---|---|
| Staff | 10 | 5 | 15 |
| Faculty | 5 | 10 | 15 |
| Totals: | 15 | 15 | 30 |
Contingency tables are often coded as below to simplify calculation of the Phi coefficient.
| Y\X | 0 | 1 | Totals |
|---|---|---|---|
| 1 | A | B | A + B |
| 0 | C | D | C + D |
| Totals: | A + C | B + D | N |
With this coding: phi = (BC - AD)/sqrt((A+B)(C+D)(A+C)(B+D)).
For this example we obtain: phi = (25-100)/sqrt(15•15•15•15) = -75/225 = -0.33, indicating a slight correlation. Please note that this is the Pearson correlation coefficient, just calculated in a simplified manner. However, the extreme values of |r| = 1 can only be realized when the two row totals are equal and the two column totals are equal. There are thus ways of computing the maximal values, if desired.
Measures of Association: C, V, Lambda
As product moment correlation coefficients, the point biserial, phi, and Spearman rho are all special cases of the Pearson. However, there are correlation coefficients which are not. Many of these are more properly called measures of association, although they are usually termed coefficients as well. Three of these are similar to Phi in that they are for nominal against nominal data, but these do not require the data to be dichotomous.One is called Pearson's contingency coefficient and is termed C whereas the second is called Cramer's V coefficient. Both utilize the chi-square statistic so will be deferred into the next lesson. However, the Goodman and Kruskal lambda coefficient does not, but is another commonly used association measure. There are two flavors, one called symmetric when the researcher does not specify which variable is the dependent variable and one called asymmetricwhich is used when such a designation is made. We leave the details to any good statistics book.
Biserial Correlation Coefficient
Another measure of association, the biserial correlation coefficient, termed rb, is similar to the point biserial, but pits quantitative data against ordinal data, but ordinal data with an underlying continuity but measured discretely as two values (dichotomous). An example might be test performance vs anxiety, where anxiety is designated as either high or low. Presumably, anxiety can take on any value inbetween, perhaps beyond, but it may be difficult to measure. We further assume that anxiety is normally distributed. The formula is very similar to the point-biserial but yet different:Tetrachoric Correlation Coefficient
The tetrachoric correlation coefficient, rtet, is used when both variables are dichotomous, like the phi, but we need also to be able to assume both variables really are continuous and normally distributed. Thus it is applied to ordinal vs.ordinal data which has this characteristic. Ranks are discrete so in this manner it differs from the Spearman. The formula involves a trigonometric function called cosine. The cosine function, in its simpliest form, is the ratio of two side lengths in a right triangle, specifically, the side adjacent to the reference angle divided by the length of the hypotenuse. The formula is: rtet =Rank-Biserial Correlation Coefficient
The rank-biserial correlation coefficient, rrb, is used for dichotomous nominal data vs rankings (ordinal). The formula is usually expressed as rrb = 2 •(Y1 - Y0)/n, where n is the number of data pairs, and Y0 and Y1, again, are the Y score means for data pairs with an x score of 0 and 1, respectively. These Y scores are ranks. This formula assumes no tied ranks are present. This may be the same as a Somer's D statistic for which an online calculator is available.Coefficient of Nonlinear Relationship (eta)
It is often useful to measure a relationship irrespective of if it is linear or not. The eta correlation ratio or eta coefficient gives us that ability. This statistic is interpretted similar to the Pearson, but can never be negative. It utilizes equal width intervals and always exceeds |r|. However, even though r is the same whether we regress y on x or x on y, two possible values for eta can be obtained.
'All the others > Statistics' 카테고리의 다른 글
| Correlation : Relationships Between Variables (0) | 2014.04.10 |
|---|---|
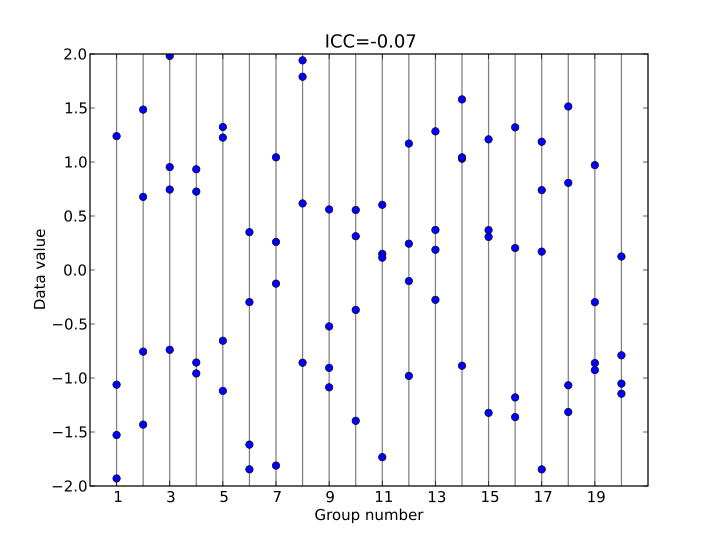
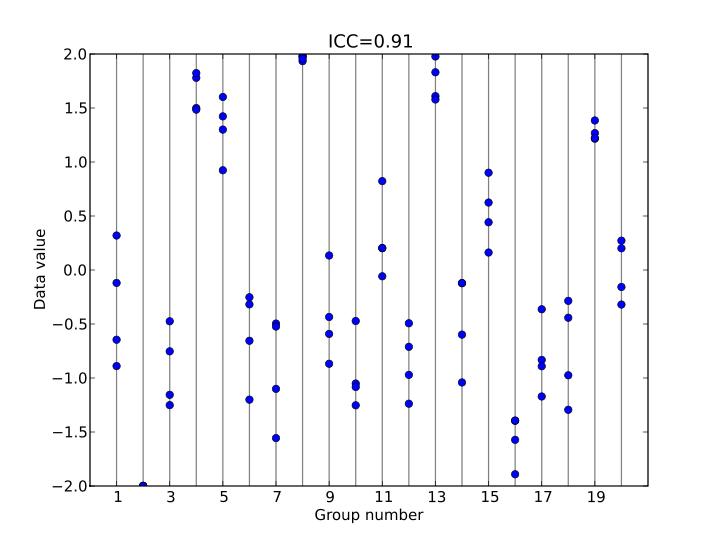
| Intraclass Correlation(ICC), Reliability, Cronbach's alpha, (0) | 2013.12.11 |
| Error bar in graphs - S.E. or S.D. (0) | 2013.09.16 |
| 타당도(Validity) (0) | 2013.08.21 |
| KOSSDA 2013년 하계 방법론 워크숍 : 중급통계학 제10일. 로지스틱 회귀분석 (Logistic Regression) (3) (3) | 2013.07.27 |






 (alpha)
(alpha)





 방법26샘플신뢰도와타당도.hwp
방법26샘플신뢰도와타당도.hwp [그림 8-11]에서는 하나의 측정하고자 하는 개념이 빗금을 친 원으로 나타나 있고 조작적 정의 1과 2가 다른 원들로 나타나 있다. 여기에 조작적 정의 1과 측정하고자 하는 개념이 완전히 일치된다면, 조작적 정의가 측정하고자 하는 개념을 완벽하게 측정하였다고 할 수 있으며, 이 때의 타당도는 1.0이라고 할 수 있다. 또한 중복되는 범위가 점점 적어지면 타당성이 적어진다고 할 수 있다.
[그림 8-11]에서는 하나의 측정하고자 하는 개념이 빗금을 친 원으로 나타나 있고 조작적 정의 1과 2가 다른 원들로 나타나 있다. 여기에 조작적 정의 1과 측정하고자 하는 개념이 완전히 일치된다면, 조작적 정의가 측정하고자 하는 개념을 완벽하게 측정하였다고 할 수 있으며, 이 때의 타당도는 1.0이라고 할 수 있다. 또한 중복되는 범위가 점점 적어지면 타당성이 적어진다고 할 수 있다. 타당성은 그 평가방법에 따라 [그림 8-12]와 같이 ① 내용타당성(content validity), ② 기준에 의한 타당성(criterion-related validity) 및 ③ 개념타당성(construct validity)의 개념으로 나누어 볼 수 있다.
타당성은 그 평가방법에 따라 [그림 8-12]와 같이 ① 내용타당성(content validity), ② 기준에 의한 타당성(criterion-related validity) 및 ③ 개념타당성(construct validity)의 개념으로 나누어 볼 수 있다.








