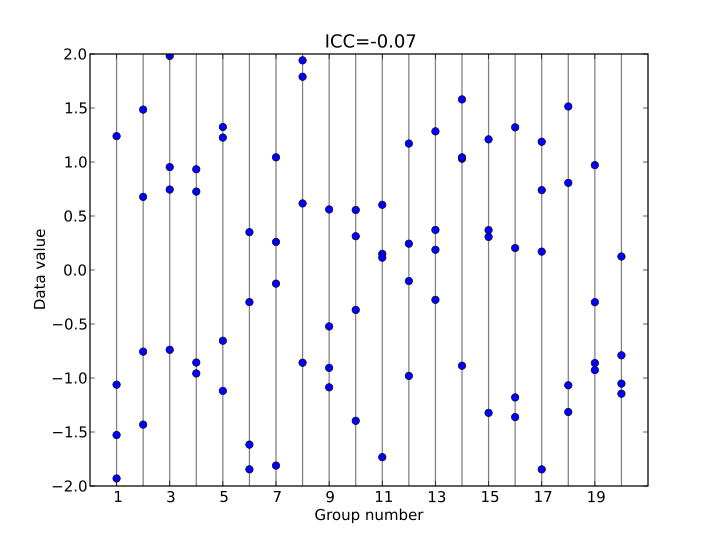
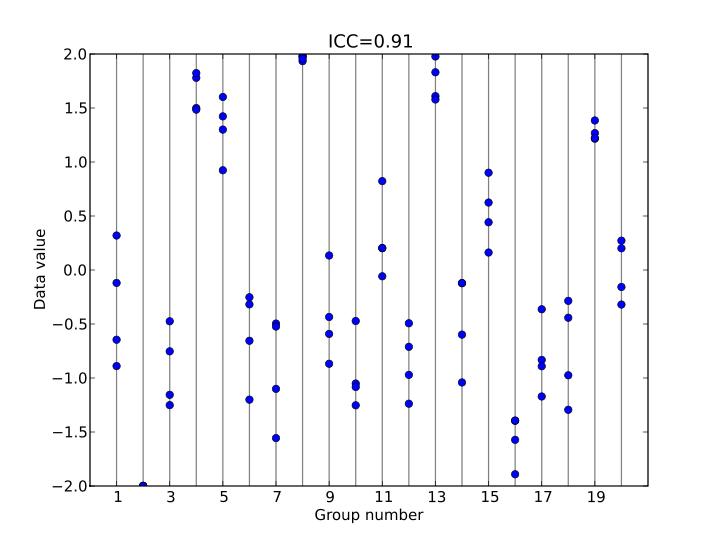
Cohen's kappa 는 평가자간 일치도를 측정하는 분석입니다. 하지만, kappa는 2명의 평가자간 일치도만 볼 수 있습니다.
그래서, 2명 이상의 평가자간 일치도를 볼 때 가장 쉬우면서도 좋은 도구로는 ICC(Intra-Class Correlation) 가 있습니다.
SAS나 SPSS에서도 바로 지원이 되기 때문에 비교적 쉽게 구할 수 있습니다.
>현재 설문지를 하나 개발중인데, 피험자들간의 문항반응일치도를 구해야 합니다.
>
>일반적으로 KAPPA를 구하면 된다고 알고 있는데, SAS와 SPSS모두 2명일 경우에만 가정하고 있네요.
>
>최근 SAS프로그램에서 multi-rater reliability구할 수 있다는데 웹을 온종일 뒤져봐도 뭔 소리인지...쉽게 구할 수 있는 방법없을까요?
>
>논문을 읽다보니 rwg(j)로도 평가자들간의 문항일치도를 확인할 수 있다는데 rwg(j)에 대한 논문은 있으나 구체적으로 어떤 프로그램으로 어떻게 구하는가에 대한 글을 찾기가 힘드네요...
>
>혹 수식따라 수작업해야 하는 것은 아닌지 ㅠ.ㅠ;;
>
>답변 급구합니다.
(http://www.statedu.com/?mid=QnA&sort_index=regdate&order_type=asc&page=192&document_srl=80652)
data 입력방법은 2번째 방식으로 사용되어져야 합니다.
분석방법은
분석 --> 척도화 분석 --> 신뢰도분석
항목 : 평가자1, 평가자2, ....
통계량 : 급내 상관계수
를 체크하시고 분석을 하면 됩니다.
... 언제나 최선을 다하는 StatEdu가 되길 빌며 ...
>안녕하세요?
>
>전화통화로 평정자간 신뢰도 구하는 방법 설명들었었는데,
>막상 직접 SPSS로 분석하려니 막혀서 질문 올립니다.
>(제가 통계에 익숙하지 않아서.... )
>
>일단, 제 자료를 말씀드리면
>교육프로그램을 만들고, 이 프로그램이 일정한 기준(A,B,C, D항목마다 각 2개질문씩)에 부합되는지를 매우 아니다(1), 아니다(2), 그렇다(3), 매우 그렇다(4) 리커트척도로 평정하게 했습니다
>
>결과 제시할 때, 각 기준에 따라 평균과 표준편차를 제시하면서, 평정자간 일치도도 같이 제시해주는 것이 좋을 것 같아서, ICC(Intra-Class Correlation)을 제시해주려고 합니다.
>
>각 항목별로 평정자간의 일치도가 어느정도인지 산출하려면,
>SPSS에서 분석할 때 변인값을 어떻게 해줘야 하는지 해서요..
>그리고, 명령어를 어떻게 해줘야 하는지 해서 문의드립니다.
>
>데이타코딩을 어떻게 해야 하는지 몰라, 두가지 형식으로 첨부합니다.
>(Spss14.0평가판 화일입니다)
>
> cf 혹시 안열릴까봐, 각 화일형식을 설명하면
>
>평정데이타1.sav의 데이타코딩은 아래와 같고요,
>
> 1A1, 1A2, 1B1, 1B2, 1C1, 1C2, 1D1, 1D2
>평정자1 2 3 3 3 3 3 2 2
>평정자2 3 4 3 4 4 4 4 2
>평정자3
> .
> .
> .
>평정자9
>
>
>평정데이타2.sav의 데이타코딩은 아래와 같습니다 .
>
> 평정자1 평정자2 평정자 3 ......... 평정자 9
> 1A1
> 1A2
> 1B1
> 1B2
> .
> .
> .
> 1D2
>
>
>
>그리고, SPSS에서 구체적으로 명령어를 어떻게 해야하는지요.
(http://www.statedu.com/?mid=QnA&page=4&sort_index=readed_count&order_type=desc&document_srl=84288)
CT에서 50명의 tumor에 대해서 longest diameter를 3명의 연구자가 측정하였다. 3명의 연구자간에 측정치가 유의하게 일치하는가?
(http://wwww.cbgstat.com/v2/method_reliability_analysis/reliability_analysis.php)
Cronbach's alpha
In statistics, Cronbach's  (alpha)[1] is a coefficient of internal consistency. It is commonly used as an estimate of the reliability of a psychometric test for a sample of examinees. It was first named alpha by Lee Cronbach in 1951, as he had intended to continue with further coefficients. The measure can be viewed as an extension of the Kuder–Richardson Formula 20 (KR-20), which is an equivalent measure for dichotomous items. Alpha is not robust against missing data. Several other Greek letters have been used by later researchers to designate other measures used in a similar context.[2] Somewhat related is the average variance extracted (AVE).
(alpha)[1] is a coefficient of internal consistency. It is commonly used as an estimate of the reliability of a psychometric test for a sample of examinees. It was first named alpha by Lee Cronbach in 1951, as he had intended to continue with further coefficients. The measure can be viewed as an extension of the Kuder–Richardson Formula 20 (KR-20), which is an equivalent measure for dichotomous items. Alpha is not robust against missing data. Several other Greek letters have been used by later researchers to designate other measures used in a similar context.[2] Somewhat related is the average variance extracted (AVE).
This article discusses the use of  in psychology, but Cronbach's alpha statistic is widely used in the social sciences, business, nursing, and other disciplines. The term item is used throughout this article, but items could be anything — questions, raters, indicators — of which one might ask to what extent they "measure the same thing." Items that are manipulated are commonly referred to as variables.
in psychology, but Cronbach's alpha statistic is widely used in the social sciences, business, nursing, and other disciplines. The term item is used throughout this article, but items could be anything — questions, raters, indicators — of which one might ask to what extent they "measure the same thing." Items that are manipulated are commonly referred to as variables.
Internal consistency
Cronbach's alpha will generally increase as the intercorrelations among test items increase, and is thus known as an internal consistency estimate of reliability of test scores. Because intercorrelations among test items are maximized when all items measure the same construct, Cronbach's alpha is widely believed to indirectly indicate the degree to which a set of items measures a single unidimensional latent construct. However, the average intercorrelation among test items is affected by skew just like any other average. Thus, whereas the modal intercorrelation among test items will equal zero when the set of items measures several unrelated latent constructs, the average intercorrelation among test items will be greater than zero in this case. Indeed, several investigators have shown that alpha can take on quite high values even when the set of items measures several unrelated latent constructs.[8][1][9][10][11][12]As a result, alpha is most appropriately used when the items measure different substantive areas within a single construct. When the set of items measures more than one construct, coefficient omega_hierarchical is more appropriate.[13][14]
Alpha treats any covariance among items as true-score variance, even if items covary for spurious reasons. For example, alpha can be artificially inflated by making scales which consist of superficial changes to the wording within a set of items or by analyzing speeded tests.
A commonly accepted[citation needed] rule of thumb for describing internal consistency using Cronbach's alpha is as follows,[15][16] however, a greater number of items in the test can artificially inflate the value of alpha[8] and a sample with a narrow range can deflate it, so this rule of thumb should be used with caution:
| Cronbach's alpha | Internal consistency |
|---|---|
| α ≥ 0.9 | Excellent (High-Stakes testing) |
| 0.7 ≤ α < 0.9 | Good (Low-Stakes testing) |
| 0.6 ≤ α < 0.7 | Acceptable |
| 0.5 ≤ α < 0.6 | Poor |
| α < 0.5 | Unacceptable |
Generalizability theory
Cronbach and others generalized some basic assumptions of classical test theory in their generalizability theory. If this theory is applied to test construction, then it is assumed that the items that constitute the test are a random sample from a larger universe of items. The expected score of a person in the universe is called the universe score, analogous to a true score. The generalizability is defined analogously as the variance of the universe scores divided by the variance of the observable scores, analogous to the concept of reliability in classical test theory. In this theory, Cronbach's alpha is an unbiased estimate of the generalizability. For this to be true the assumptions of essential  -equivalence or parallelness are not needed. Consequently, Cronbach's alpha can be viewed as a measure of how well the sum score on the selected items capture the expected score in the entire domain, even if that domain is heterogeneous.
-equivalence or parallelness are not needed. Consequently, Cronbach's alpha can be viewed as a measure of how well the sum score on the selected items capture the expected score in the entire domain, even if that domain is heterogeneous.
Intra-class correlation
Cronbach's alpha is said to be equal to the stepped-up consistency version of the intra-class correlation coefficient, which is commonly used in observational studies. But this is only conditionally true.
In terms of variance components, this condition is, for item sampling: if and only if the value of the item (rater, in the case of rating) variance component equals zero.
If this variance component is negative, alpha will underestimate the stepped-up intra-class correlation coefficient;
if this variance component is positive, alpha will overestimate this stepped-up intra-class correlation coefficient.
Factor analysis
Cronbach's alpha also has a theoretical relation with factor analysis. As shown by Zinbarg, Revelle, Yovel and Li,[14] alpha may be expressed as a function of the parameters of the hierarchical factor analysis model which allows for a general factor that is common to all of the items of a measure in addition to group factors that are common to some but not all of the items of a measure. Alpha may be seen to be quite complexly determined from this perspective. That is, alpha is sensitive not only to general factor saturation in a scale but also to group factor saturation and even to variance in the scale scores arising from variability in the factor loadings. Coefficient omega_hierarchical[13][14] has a much more straightforward interpretation as the proportion of observed variance in the scale scores that is due to the general factor common to all of the items comprising the scale.
(http://en.wikipedia.org/wiki/Cronbach's_alpha)
Intraclass correlation
In statistics, the intraclass correlation (or the intraclass correlation coefficient, abbreviated ICC)[1] is a descriptive statistic that can be used when quantitative measurements are made on units that are organized into groups. It describes how strongly units in the same group resemble each other. While it is viewed as a type of correlation, unlike most other correlation measures it operates on data structured as groups, rather than data structured as paired observations.
The intraclass correlation is commonly used to quantify the degree to which individuals with a fixed degree of relatedness (e.g. full siblings) resemble each other in terms of a quantitative trait (see heritability). Another prominent application is the assessment of consistency or reproducibility of quantitative measurements made by different observers measuring the same quantity.
Relationship to Pearson's correlation coefficient
In terms of its algebraic form, Fisher's original ICC is the ICC that most resembles the Pearson correlation coefficient. One key difference between the two statistics is that
in the ICC, the data are centered and scaled using a pooled mean and standard deviation, whereas in the Pearson correlation, each variable is centered and scaled by its own mean and standard deviation.
This pooled scaling for the ICC makes sense because all measurements are of the same quantity (albeit on units in different groups).
For example, in a paired data set where each "pair" is a single measurement made for each of two units (e.g., weighing each twin in a pair of identical twins) rather than two different measurements for a single unit (e.g., measuring height and weight for each individual), the ICC is a more natural measure of association than Pearson's correlation.
An important property of the Pearson correlation is that it is invariant to application of separate linear transformations to the two variables being compared. Thus, if we are correlating X and Y, where, say, Y = 2X + 1, the Pearson correlation between X and Y is 1 — a perfect correlation.
This property does not make sense for the ICC, since there is no basis for deciding which transformation is applied to each value in a group. However if all the data in all groups are subjected to the same linear transformation, the ICC does not change.
Use in assessing conformity among observers
The ICC is used to assess the consistency, or conformity, of measurements made by multiple observers measuring the same quantity.[8]
For example, if several physicians are asked to score the results of a CT scan for signs of cancer progression, we can ask how consistent the scores are to each other.
If the truth is known (for example, if the CT scans were on patients who subsequently underwent exploratory surgery), then the focus would generally be on how well the physicians' scores matched the truth. If the truth is not known, we can only consider the similarity among the scores.
An important aspect of this problem is that there is both inter-observer and intra-observer variability.
Inter-observer variability refers to systematic differences among the observers — for example, one physician may consistently score patients at a higher risk level than other physicians.
Intra-observer variability refers to deviations of a particular observer's score on a particular patient that are not part of a systematic difference.
The ICC is constructed to be applied to exchangeable measurements — that is, grouped data in which there is no meaningful way to order the measurements within a group.
In assessing conformity among observers, if the same observers rate each element being studied, then systematic differences among observers are likely to exist, which conflicts with the notion of exchangeability. If the ICC is used in a situation where systematic differences exist, the result is a composite measure of intra-observer and inter-observer variability.
One situation where exchangeability might reasonably be presumed to hold would be where a specimen to be scored, say a blood specimen, is divided into multiple aliquots, and the aliquots are measured separately on the same instrument. In this case, exchangeability would hold as long as no effect due to the sequence of running the samples was present.
Since the intraclass correlation coefficient gives a composite of intra-observer and inter-observer variability, its results are sometimes considered difficult to interpret when the observers are not exchangeable. Alternative measures such as Cohen's kappa statistic, the Fleiss kappa, and the concordance correlation coefficient[9] have been proposed as more suitable measures of agreement among non-exchangeable observers.
Calculation in software packages[edit]
ICC is supported by the R software package (using the icc command with packages psy, psych or irr). Non-free software also supports ICC, for instance Stata orSPSS [10]
| Shrout and Fleiss convention | Name in SPSS |
|---|---|
| ICC(1,1) | One-way random single measures |
| ICC(1,k) | One-way random average measures |
| ICC(2,1) | Two-way random single measures (Consistency/Absolute agreement) |
| ICC(2,k) | Two-way random average measures (Consistency/Absolute agreement) |
| ICC(3,1) | Two-way mixed single measures (Consistency/Absolute agreement) |
| ICC(3,k) | Two-way mixed average measures (Consistency/Absolute agreement) |
'All the others > Statistics' 카테고리의 다른 글
| 상관계수의 종류(Point-Biserial, Biserial Correlation, etc.) (1) | 2014.04.11 |
|---|---|
| Correlation : Relationships Between Variables (0) | 2014.04.10 |
| Error bar in graphs - S.E. or S.D. (0) | 2013.09.16 |
| 타당도(Validity) (0) | 2013.08.21 |
| KOSSDA 2013년 하계 방법론 워크숍 : 중급통계학 제10일. 로지스틱 회귀분석 (Logistic Regression) (3) (3) | 2013.07.27 |