다중 비교에 관한 팩트와 픽션(J Grad Med Educ, 2021)
Facts and Fictions About Handling Multiple Comparisons
Gail M. Sullivan, MD, MPH
Richard S. Feinn, PhD

한 가지 측면은 많은 비교를 이용한 분석과 관련이 있다. 다중 독립 비교를 고려하지 않는 교육자와 연구자는 다음과 같은 검토자의 의견을 받을 수 있다.
- 얼마나 많은 비교를 할 계획이었나요?
- 이러한 다중 비교를 위해 어떻게 조정했습니까? 또는
- 다중 비교가 통계적 추론에 어떤 영향을 미칩니까?
One aspect concerns analyses using many comparisons. Educators and researchers who do not take into account multiple independent comparisons may receive reviewer comments such as:
- Where did you prespecify how many comparisons you planned to make?
- How did you adjust for these multiple comparisons? or
- How do the multiple comparisons affect your statistical inferences?
다중 비교를 고려하지 않으면 내부 타당성에 대한 의문이 제기될 수 있습니다(즉, 이러한 결과가 실제로 사실입니까?). 또한 검토자와 저자의 관점에서 저자에 대한 신뢰도를 낮출 수 있다(이 작가들은 그들이 뭘 하는지 알고 있을까? )임상의와 교육자로서 우리는 이러한 문제와 투명하고 잘 다루지 않을 경우 연구나 논문을 파멸시킬 수 있는 방법에 대해 잘 알지 못할 수 있다.
Not considering multiple comparisons can raise questions of internal validity (ie, are these findings actually true?). It can also lower, in the minds of reviewers and authors, confidence in the authors: Do these authors know what the heck they're doing? As clinicians and educators we may be less aware of these issues and how they can doom a study or paper if not handled transparently and well.
정량적 논문을 고려할 때 다음과 같은 3가지 질문이 즉시 제기된다.
- (1) 본 논문은 내 환경 또는 교육생(외부 타당성, 일반화 가능성)에 적용되는가?
- (2) 연구 대상 전체 모집단에 대한 우연 또는 사실로 인한 발견인가(위양성 대 실제 양성 발견) 및
- (3) 소견의 크기 또는 의미(효과 크기)는 어느 정도인가?1
이 사설은 많은 작가들에게 성배인 두 번째 이슈에 대해 간략하게 소개합니다: 상당한 P 레벨입니다.
When considering a quantitative paper, 3 questions immediately arise:
- (1) Does this paper apply to my setting or trainees (external validity, generalizability);
- (2) Are the findings likely due to chance or true for the overall population being studied (false vs true positive finding); and
- (3) How large or meaningful are the findings (effect size).1
This editorial provides a brief introduction to the second issue, the holy grail for many authors: a significant P level.
기본으로 돌아가기
Back to Basics
왜 우리는 P 레벨을 소중히 여기는가? 두 평균을 비교하는 단일 비교부터 시작합시다. 내과 레지던트 그룹이 고가의 이사회 검사 준비 과정을 수강했지만 유사한 레지던트 그룹이 수강하지 않았다고 가정하고, 그룹 간 이사회 점수 평균을 비교하여 이 과정을 계속 진행해야 하는지 여부를 결정하려고 합니다. 귀무 가설이 참이라고 가정하면(즉, 그룹 간에 차이가 없다), P 값은 선택된 거주자(모든 전공의의 무작위 표본)가 적어도 발견된 크기의 두 가지 이사회 점수 수단에서 차이를 생성할 확률이다.
Why do we cherish P levels? Let's start with a single comparison, comparing 2 means. Suppose a group of internal medicine residents took an expensive board examination prep course and a similar group of residents did not, and we want to compare board score means between groups to determine if the course should be continued. If we assume that the null hypothesis is true (ie, there is no difference between the groups), the P value is the probability that our selection of residents—a random sample of all residents—produced a difference in the 2 board score means of at least the size found.
제1종 오류(alpha)는 연구팀이 합당하다고 인정하는 오류의 수준으로, 통계시험을 실시하기 전에 이를 선택해야 한다. 즉, 실제로 차이가 없을 때 그룹 간에 차이가 존재한다고 결론을 내릴 확률이다. 통계 테스트의 P 수준이 선택한 오류 수준보다 작은 경우(보통 5%(0.05)), 테스트 차이는 보드 준비 과정이 아니라 전공의의 선택으로 인해 발견된 차이(전체 모집단을 연구할 수 없기 때문에)일 5%의 확률만 갖는 것으로 본다. (즉, 시험 점수 차이가 우리 연구를 위해 선택된 거주자 때문에 발생할 5% 확률, 즉 우연에 의해서만 발생).
Type I error (alpha) is the error level deemed reasonable by the research team, who must select it before conducting the statistical test. It is the probability of committing a false positive error: in other words, of concluding that a difference between groups exists when there is truly no difference. If the P level from the statistical test is less than the selected error level, usually 5% (.05), we view the test difference as having only a 5% chance that the difference found is due to the selection of residents (as we cannot study the entire population) rather than the board prep course (ie, a 5% chance that the test score difference is due to the residents selected for our study, ie, by chance alone).
하지만 이 값비싼 이사회 준비 과정의 대상이 누구인지를 이해하는 데 중요한 추가 요소를 살펴보려면 어떻게 해야 할까요? 예: 교육 중 시험 점수, 레지던트 나이 및 성별, 미국 의대 졸업자 대 국제 의대 졸업자, 레지던트 중 마일스톤 등급(Milestones leveling) 또는 선호되는 아침식사 음료? 우리가 환자를 위한 많은 실험실 검사를 주문할 때도 이러한 문제가 발생할 수 있습니다.
But what if we wish to look at additional factors that might be important to understanding who should be targeted for this expensive board prep course? For example: in-training examination scores, resident age and gender, US medical graduate vs international medical graduate, Milestones ratings during residency—or preferred breakfast drink? These issues can occur when we order many lab tests for a patient, too.
알파 또는 I형 오류 수준이 비교 시마다 0.05로 유지되면 하나 이상의 "통계적으로 유의한" 결과가 나올 확률은 5% 이상 증가합니다(그림 참조). 예를 들어, 10개의 비교의 경우 검사 중인 요인이 아닌 랜덤하게 선택된 주민 모집단(즉, 우연히)으로 인해 적어도 하나의 "통계적으로 유의한"(P < .05) 비교를 찾을 확률이 40%로 증가합니다.
13개의 독립적인 비교의 경우, 우연히 "유의한" P 수준을 찾을 확률은 50%로 증가합니다.2 이러한 값을 familywise error rate이라고 하며, 이는 family of comparison에 의해 발생한다.
If the alpha or type I error level remains at .05 for each comparison, the probability of at least one finding being “statistically significant” increases above 5% (see Figure). For example, for just 10 comparisons, the probability rises to 40% that you will find at least one “statistically significant” (P < .05) comparison that is due to the population of residents randomly selected rather than the factor under examination—that is, by chance. For 13 independent comparisons, the probability of finding a “significant” P level by chance increases to 50%.2 These are called family-wise error rates, for a family of comparisons.
아침 식사로 차를 마시는 전공의가 이 보드 준비 과정을 수강하는 데 가장 적합한 대상이라고 잘못 결론을 내릴 수 있는 것이다.
You could erroneously conclude that residents who drink tea for breakfast are the best target for taking this board prep course—and create tortured explanations for this finding in your Discussion section.

통계적 유요성은 허용 오차 수준(알파 또는 유형 I 오류)에 의해 결정되며, 표본 모집단이 전체 모집단과 유사할 가능성(예: 여러 기관에서 2020-2021년 내과 레지던트들이 모든 내과 레지던트들과 유사)을 반영한다는 점을 기억하라. 이 다중 비교 문제는 95% 신뢰 구간과도 관련이 있습니다. 다중 비교를 수행하고 각 비교에 대해 평균 차이의 95% 신뢰 구간을 생성하면 모든 구간에 평균의 실제 차이가 포함될 확률은 95% 미만입니다.
Remember that statistical significance is determined by the level of error accepted (alpha or type I error) and reflects the likelihood that the sampled population resembles the entire population (eg, that internal medicine residents in 2020–2021 at several institutions resemble all internal medicine residents). Note that this issue of multiple comparisons also pertains to 95% confidence intervals. If multiple comparisons are performed and a 95% confidence interval of the difference in means is created for each comparison, the probability that all the intervals will contain the true difference in means will be less than 95%.
극단적인 예로, 게놈 전체 연관 연구(GWAS)를 수행하는 연구자들이 다중 테스트에 적응하지 않았다고 가정해 보자. GWAS는 질병과의 연관성에 대해 100,000개의 다른 위치를 검사할 수 있다. 각 위치에 0.05의 알파 수준을 사용한 경우 위양성 값이 많이 나올 수 있습니다.
As an extreme example, imagine if researchers conducting genome-wide association studies (GWAS) did not adjust for multiple testing. GWAS may test 100 000 different loci for an association with a disease. If an alpha level of .05 was used for each locus you can guarantee there would be numerous false positives.
낚시 원정대 및 P-해킹
Fishing Expeditions and P-Hacking
낚시 탐험대 또는 [P-해킹]이라는 용어는 연구자들이 독립변수와 종속변수의 관계에 대한 모든 가능한 비교에 대해 그들의 데이터를 검사할 때를 가리킨다.
- 독립 변수(예: 인구통계학적 요인, 대학원생 수준, 전문성, 학부 위치, 레지던트 순환)
- 종속 변수(예: 웰빙 지수, 번아웃 지수, 번아웃 서브그룹 요소, 워라밸 지수)
더 많이 비교할수록 P 수준 < .05가 비교 대상으로 발견될 가능성이 높으며, 귀무 가설(즉, 차이 없음)은 부정확하게 기각될 수 있다. 이 용어들은 일반적으로 경멸적이며, 예를 들어 논문의 요약 또는 결과 섹션과 같이 중요한 결과만 보고되는 경우를 위해 남겨둔다.
The terms fishing expedition or P-hacking refer to when researchers examine their data for every possible comparison of independent variables (eg, numerous demographic factors, postgraduate year levels, specialties, undergraduate locations, residency rotations) and/or dependent variables (eg, well-being index, burnout index, burnout subgroup elements, work-life balance index). The more comparisons, the more likely a P level of < .05 will be found for a comparison, and the null hypothesis (ie, no difference) may be rejected inaccurately. These terms are generally pejorative and reserved for when only the significant findings are reported, for example in the Abstract or Results section of a paper.
이 문제는 [흥미로운 발견을 어디서 찾을 수 있을지에 대한 기대 없이 완전히 새로운 질문을 탐구할 때]에는 피할 수 없을지도 모른다. 그러나 의학 교육에서 이것은 거의 사실이 아니다; 우리는 보통 이전의 연구나 그럴듯한 이론에 근거한 가설을 가지고 있다. '낚시'가 나타나는 것을 피하려면 '방법' 섹션에서 자신의 접근 방식에 대한 문헌과 이론적 틀을 바탕으로 계획된 비교를 미리 규정하는 것이 최선이다. 이 fishing의 문제는 임상시험에서 충분히 자주 발견되어 이제 연구자들이 데이터를 수집하고 분석하기 전에 주요 결과물을 공공 사이트(clinicaltrials.gov)에 게시하는 것이 의무화 되었다. 데이터를 본 후에는 분석을 추가하고 싶은 유혹을 이겨내십시오!
This problem may be inevitable when exploring entirely new questions with no expectation of where the interesting findings may lie. However, in medical education this is rarely true; we usually have hypotheses based on prior work or plausible theory. To avoid the appearance of “fishing,” it is best to prespecify, based on the literature and theoretical framework for your approach, your planned comparisons in the Methods section. This fishing problem was found often enough in clinical trials that it is now mandatory for researchers to post the primary outcome(s) on a public site (clinicaltrials.gov) before the data are collected and analyzed. Resist the temptation to add additional analyses after you have seen the data!
그럴듯한 사전 가설이 없는 경우 많은 비교를 수행하고, 관련된 P 수준 및 신뢰 구간과 함께 모든 가설을 보고하고, 방법 절에 탐색 가설이며, 이러한 이유로 다중 비교를 조정하지 않았다고 기술할 수 있습니다. 검정 횟수가 증가함에 따라 모임별 오류율도 증가하므로 이러한 상황에서는 추론을 그리는 데 주의해야 합니다.
When there are no plausible prior hypotheses, it can be acceptable to make many comparisons, report all of them with the associated P levels and/or confidence intervals, and state in your Methods section that these were exploratory hypotheses and that no adjustment for multiple comparisons was made for this reason. Be cautious in drawing inferences in these situations: as the number of tests expands, so does the family-wise error rate.
비교 및 사전 계획 분석을 제한하는 이유
Why to Limit Comparisons and Pre-Plan Analyses
프로젝트를 준비하기 위한 첫 번째 단계는 문헌에 대한 심층적인 검토입니다.
- 다른 연구자들은 어떤 방법을 사용했나요?
- 어떤 이론이 다른 접근법을 뒷받침할 수 있는가?
- 우리의 지식에는 어떤 gap이 있을까요?
In preparing for a project, the first step is a deep dive into the literature:
- What methods did other researchers use?
- What theories may support different approaches?
- What gaps remain in our knowledge?
종종 이전 작업은 다음 단계로 구체적인 방향이나 질문을 제공합니다. 따라서 계획된 데이터 분석뿐만 아니라 데이터 수집도 제한할 수 있습니다. 데이터가 이미 수집되었다면(예: 의학대학원 교육 인증 위원회 및 국가 프로그램 관리자 그룹에는 방대한 데이터 수집이 있다), 질문에 답변하는 데 필요한 사항을 신중하게 선택하십시오.
Often prior work will provide you with specific directions or questions as next steps. This in turn will help you limit the collection of data as well as planned analyses of the data. If data were already collected (eg, Accreditation Council for Graduate Medical Education and national program director groups have enormous data collections to explore), choose carefully what you need to answer your question(s).
여기 문제가 있다: 다중 비교를 수정하지 않으면 복제 스터디에서 다른 연구자는 발견하지 못하는 위양성 결과를 찾을 위험이 있습니다. 다중 비교를 수정하면 실제로 존재하는 차이를 찾을 수 있는 통계적 검정력이 손실됩니다(위음성). 따라서, 당신의 질문에 가장 적합한 것으로 당신의 비교를 제한하세요.
Here's the conundrum: If you don't correct for multiple comparisons, you risk finding “significant” results that are false positives and that will not be found by others in replication studies. If you do correct for multiple comparisons, you lose statistical power to find differences that actually exist (false negatives). Ergo, limit your comparisons to what fits your questions best.
비교에 대한 수정이 필요하지 않은 경우도 있습니다. 예를 들어, [새로운 경험적 오리엔테이션 프로그램]이 현재 [미국 정신건강의학 인턴]에서 [6개월째에 집계된 전문직업성 마일스톤]에 미치는 영향을 보고 있다고 생각해 보십시오. 인턴들 중 절반은 새로운 일주일간의 체험 오리엔테이션을 받고, 나머지 절반은 대규모 그룹 오리엔테이션과 가상 오리엔테이션을 병행한다. 경험적 오리엔테이션 프로그램을 받은 사람들은 P < .05 수준에서 유의미하게 더 높은 점수를 받는다.
Correction for a comparison may not be needed in some instances. For example, consider that you are looking at the effects of a new experiential orientation week on intern performance on aggregated professionalism milestones at 6 months, in current US psychiatry interns. Half of the interns receive the new week-long experiential orientation, and the other half receive a combination of large group and virtual orientation sessions. Those with the experiential orientation score significantly (and meaningfully) higher at the P < .05 level.
아래의 하위그룹에 대해서 이차 분석을 계획합니다.
- 국제 의학 졸업생 대 미국 의학 졸업생,
- 남자 대 여자,
- 나이가 많은(30세) 대 어린(31세),
- USMLE 1단계 5분위수 및
- 대학 기반 프로그램과 비대학 기반 프로그램의 사용자.
You plan secondary analyses to look at subgroups:
- international medical graduates vs US medical graduates,
- male vs female,
- older (> 30) vs younger (< 31 years),
- USMLE Step 1 quintile, and
- those at university-based vs non-university-based programs.
이 예에서는 2차 분석에서는 다중 비교를 위해 조정이 필요할 수 있지만, 1차 분석에서는 correction이 필요하지 않다.
In this example, it is not necessary to correct for the primary analysis, although the secondary analyses may require adjustment for multiple comparisons.
다중 비교 처리 전략
Strategies for Handling Multiple Comparisons
계획 중인 가장 중요한 비교를 고려한 후 여러 개 이상의 비교를 수행할 경우 다중 비교를 반영하도록 분석을 조정하는 것을 고려해야 합니다. 비교할 항목을 결정하기 전에 데이터를 살펴본다면 이미 다중 비교를 수행한 것입니다. 우리는 당신이 진정으로 탐구적인 연구를 수행하는 것이 아니라면 이것을 하지 말 것을 제안합니다.
After considering the most important comparisons you plan to make, if you have more than a few, you should consider adjusting your analysis to reflect the multiple comparisons. (Remember that if you look at your data before deciding what comparisons to make, you have already made multiple comparisons. We suggest not to do this unless you are performing truly exploratory research.)
고려해야 할 많은 방법들이 있고, 전문은 물론 수많은 글들이 잘 묘사되어 있다. 이 가운데 본페로니 교정은 의학 교육에 많이 쓰인다. 본페로니 교정은 알파를 계획된 비교 횟수로 나누어 알파 수준(오류)을 하향 조정한다. 10개 비교의 경우 유형 I 오차가 0.05인 경우 수정된 알파 수준은 .05/10 또는 .005입니다. 이를 비교 오류율이라고도 합니다. 본페로니 교정은 기억하기 쉬워서 인기가 있지만, 특히 협회가 사실 서로 독립적이지 않을 경우 지나치게 보수적이다. 따라서 유형 II 오류(위음성)로 이어질 수 있다. 이 일반적인 접근법에는 많은 수정 사항이 있으며, 일부는 덜 보수적인 조정을 사용한다(예: 벤자미니-호흐버그 방법)은 일차 가설과 이차 가설의 알파 수준을 변화시키거나 모든 검정의 알파 수준을 더 낮은 알파 수준으로 변화시킨다(예: 0.05 대신 0.01).
There are many methods to consider, and full texts as well as numerous articles describe them well. Of these, the Bonferroni correction is often used in medical education. The Bonferroni correction adjusts the alpha level (error) downward by dividing alpha by the planned number of comparisons. For 10 comparisons, with a type I error of 0.05, the corrected alpha level is .05/10 or .005. This is sometimes termed the comparison-wise error rate. The Bonferroni correction is easy to remember and thus popular, but it is overly conservative, especially if the associations are not in fact independent of each other. Thus, it can lead to a type II error (falsely accepting the null hypothesis of no association). There are many modifications of this general approach; some include using a less conservative adjustment (eg, Benjamini–Hochberg method), varying the alpha level for primary and secondary hypotheses, or switching to a lower alpha level for all tests (eg, .01 instead of .05).
하지만 우리가 비교하고자 하는 다양한 비교가 서로 독립적이지 않다면 어떨까요? 아니면 우리가 25와 같이 많은 수의 비교를 한다면 어떨까요? 독립 변수 및 종속 변수가 상관관계가 있는 경우와 수많은 검정이 수행되는 상황에 대한 방법이 있습니다. 이 소개 기사의 범위를 벗어나, 독자들이 다중 비교와 방법을 지원할 수 있는 다양한 접근 방식에 대해 자세히 알아볼 수 있는 좋은 자료가 많이 있습니다(자료 참조).
But what if the various comparisons we want to make are not independent of each other? Or what if we are making a large number of comparisons, such as 25? There are methods for when independent and/or dependent variables are correlated and situations where numerous tests are performed. While beyond the scope of this introductory article, there are many good resources for readers to learn more about multiple comparisons and the various approaches that can support your methods (see Resources).
제한 사항에 대해 논의하는 방법
How to Discuss in Limitations
지금까지 살펴본 바와 같이, 데이터를 조사하기 전에(최적으로 데이터를 수집하기 전에) 결정을 내려야 하며, 이러한 결정이 결과의 "진실truth"에 영향을 미칠 수밖에 없습니다. 방법 섹션에서 비교 및 알파 오차 수준을 선택하여 추론을 명확하게 제시합니다. 그런 다음 토론 섹션에서 잘못된 긍정(우연히 관측된 차이) 또는 잘못된 부정(존재하나 찾지 못한 차이) 중 어느 방향으로든 결정이 결과에 영향을 미칠 수 있는 방법을 고려하십시오. 이 후자의 문제는 유형 II 오류(베타)의 결과로 더 자주 발생하며, 우리는 이를 다음 논의를 위해 저장해 둘 것이다. 방법의 결정으로 인한 잠재적 효과를 투명하게 나열하면 검토자, 편집자 및 독자의 관점에서 신뢰성이 향상되며, 장황할 필요도 없습니다. '지나친' 투명성은 '너무 적게'은 투명성보다 좋고, 과도한 단어는 개정 과정에서 싹쓸이할 수 있다.
As you have seen, decisions must be made before examining your data—optimally before even collecting your data—that will inevitably affect the “truth” of your findings. Clearly present your reasoning in choice of comparisons and alpha error levels in the Methods section. Then, in the Discussion section, consider how your decisions may have affected your findings in either direction: false positives (differences observed that are actually due to chance) or false negatives (no difference found when one does exist). This latter problem more often occurs as a result of a type II error (beta), which we will save for another discussion. Laying out the potential effects of your methods' decisions in a transparent way enhances credibility in the eyes of reviewers, editors, and readers, and does not have to be lengthy. It's better to have “too much” transparency vs “too little,” and any excess words can be trimmed away in the revision process.
결론들
Conclusions
이 기사는 의학교육연구에서 다중비교라는 주제를 거의 다루지 않는다. 교육자와 연구자들이 발표나 출판을 위해 기사를 읽고, 분석을 고려하고, 작품을 작성할 때 이 문제를 염두에 둘 수 있도록 인지도를 높였으면 한다. 가장 중요한 항목:
This article barely scratches the surface of the topic of multiple comparisons in medical education research. We hope to raise awareness so that educators and researchers keep this issue in mind when reading articles, considering analyses, and writing up their work for presentations or publications. Most important:
- 시작할 때 비교를 미리 계획합니다. 아직 분석하지 않았지만 분석을 수행하기 전에 데이터를 검토한 경우에는 이러한 사후 분석을 가능한 모든 비교로 간주하십시오.
- 비교가 서로 독립적일 가능성이 높은지 또는 일부 비교가 서로 관련이 있을 수 있는지 판단합니다.4
- 여러 가지 비교를 위해 알파 수준(오차)을 조정하는 것을 고려해 보십시오.
- 방법 섹션에서 결정을 명확하게 제시합니다.
- 자신의 방법이 토론에서 발견한 내용에 어떤 영향을 미쳤는지 토론합니다.
- 의심스러울 때는 친절한 생물통계학자 한 명에게 물어보세요.
- Preplan your comparisons at the start. If you have not, but have examined the data before deciding which analyses to make, consider these post-hoc analyses as all possible comparisons.
- Decide if your comparisons are likely independent of each other or if some may be related to each other.4
- Consider adjusting your alpha level (error) for more than a few comparisons.
- Present your decisions clearly in the Methods section.
- Discuss how your methods may have affected your findings in the Discussion.
- When in doubt, ask a friendly biostatistician.
A general introduction to adjustment for multiple comparisons
Shi-Yi Chen,1 Zhe Feng,2 and Xiaolian Yi3
Abstract
In experimental research a scientific conclusion is always drawn from the statistical testing of hypothesis, in which an acceptable cutoff of probability, such as 0.05 or 0.01, is used for decision-making. However, the probability of committing false statistical inferences would considerably increase when more than one hypothesis is simultaneously tested (namely the multiple comparisons), which therefore requires proper adjustment. Although the adjustment for multiple comparisons is proposed to be mandatory in some journals, it still remains difficult to select a proper method suitable for the various experimental properties and study purposes, especially for researchers without good background in statistics. In the present paper, we provide a brief review on mathematical framework, general concepts and common methods of adjustment for multiple comparisons, which is expected to facilitate the understanding and selection of adjustment methods.
Introduction
The statistical inference would be a critical step of experimental researches, such as in medicine, molecular biology, bioinformatics, agricultural science, etc. It is well acceptable that an appropriate significance level α, such as 0.05 or 0.01, is pre-specified to guarantee the probability of incorrectly rejecting a single test of null hypothesis (H0) no larger than α. However, there are many situations where more than one or even a large number of hypotheses are simultaneously tested, which is referred to as multiple comparisons (1). For example, it is common in clinical trials to simultaneously compare the therapeutic effects of more than one dose levels of a new drug in comparison with standard treatment. A similar problem is to evaluate whether there is difference between treatment and control groups according to multiple outcome measurements. Due to rapid advances of high-throughput sequencing technologies, it is also common to simultaneously determine differential expression among tens of thousands of genes.
The statistical probability of incorrectly rejecting a true H0 will significantly inflate along with the increased number of simultaneously tested hypotheses. In the most general case where all H0 are supposed to be true and also independent with each other, the statistical inference of committing at least one incorrect rejection will become inevitable even when 100 hypotheses are individually tested at significance level α=0.05 (Figure 1). In other words, if we simultaneously test 10,000 true and independent hypotheses, it will incorrectly reject 500 hypotheses and declare them significant at α=0.05. Of course, estimation of error rate would become more complex when hypotheses are correlated in fact and not all of them are true. Therefore, it is obvious that the proper adjustment of statistical inference is required for multiple comparisons (2). In the present paper, we provide a brief introduction to multiple comparisons about the mathematical framework, general concepts and the wildly used adjustment methods.
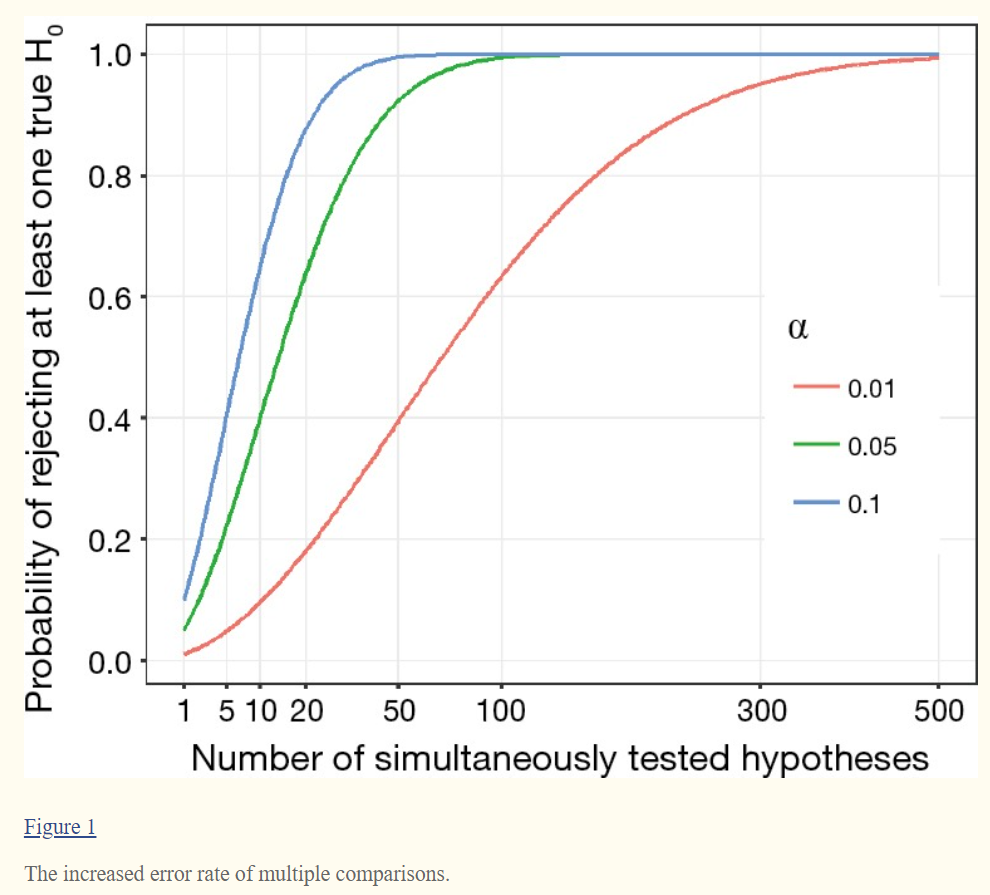
Mathematical framework
For a simultaneous testing of m hypotheses, the possible outcomes are listed in Table 1. Let’s suppose that the number of true H0 is m0, which is an unobservable random variable (0≤m0≤m). After performing statistical inferences we totally found R H0 being rejected and declared significant at the pre-specified significance level; and herein R is an observable random variable (0≤R≤m). Among the statistically rejected hypotheses of R, when R>0, we suppose that there are U H0 that have been incorrectly rejected. Similar to m0, U is also an unobservable random variable with equal to or larger than 0. Accordingly, counts of other possible outcomes could be deduced, including the correctly rejected H0 (R- U), correctly retained H0 (m0-U), and incorrectly retained H0 (m-R-m0+U).

Type I and II errors
For the statistical inference of multiple comparisons, it would commit two main types of errors that are denoted as Type I and Type II errors, respectively. The Type I error is that we incorrectly reject a true H0, whereas Type II error is referred to a false negative. Because the exact numbers of Type I and Type II errors are unobservable (as denoted in Table 1), we would intend to control the probability of committing these errors under acceptable levels. In general, the controlled probabilities of committing Type I and Type II errors are negatively correlated, for which therefore we must determine an appropriate trade-off according to various experimental properties and study purposes. If a significant conclusion has important practical consequence, such as to declare an effective new treatment, we would control Type I error more rigorously. On the other hand, we should avoid committing too many Type II errors when it intends to obtain primary candidates for further investigation, which is very common in studies of genomics. Here, we specially address the controlling of Type I error because it considerably increases for multiple comparisons.
Adjusted P value or significance level
In statistical inference, a probability value (namely P value) is directly or indirectly computed for each hypothesis and then compared with the pre-specified significance level α for determining this H0 should be rejected or not (3). Therefore, there are two ways for adjusting the statistical inference of multiple comparisons.
- First, it could directly adjust the observed P value for each hypothesis and keep the pre-specified significance level α unchanging; and this is herein referred to as the adjusted P value.
- Second, an adjusted cut-off corresponding to the initially pre-specified α could be also computationally determined and then compared with the observed P value for statistical inference.
In general, the adjusted P value is more convenient because in which the perceptible significance level is employed. However, it would be difficult or impossible to accurately compute the adjusted P value in some situations.
Measures accounting for Type I error
According to possible outcomes of multiple comparisons (Table 1), all efforts would be paid to the control of variable U, for which therefore various statistical measures have been proposed to account (4). Certainly, each of these measures has differential applications with respective strengths and weaknesses.
A simple and straightforward measurement is the expected proportion of variable U among all simultaneously tested hypotheses of m, which is referred to as the per-comparison error rate (PCER):

If each hypothesis is separately tested at significance level α, PCER will be equal to α when all H0 are true and independent with each other. Obviously, it becomes PCER=αm0/m≤α when not all H0 are true in fact. However, control of PCER would be less efficient because we would obtain at least one false positive at significance level α=0.05 when 20 true H0 are simultaneously tested.
In practical applications, it is more reasonable to jointly consider all hypotheses as a family for controlling Type I error; and therefore the most stringent criterion is to guarantee that not any H0 is incorrectly rejected. Accordingly, the measure of familywise error rate (FWER) is introduced and defined as the probability of incorrectly rejecting at least one H0:

The control of FWER has been widely used especially when only a few or at most several tens of hypotheses are simultaneously tested. However, FWER is believed to be too conservative in cases that the number of simultaneously tested hypotheses reaches several hundreds or thousands.
Another popular measure for controlling Type I error of multiple comparisons is the false discovery rate (FDR), which is defined as the expected proportion of incorrectly rejected H0 among all rejections:

Therefore, FDR allows the occurrence of Type I errors under a reasonable proportion by taking the total number of rejections into consideration. An obvious advantage of FDR controlling is the greatly improved power of statistical inference, which would be useful when a large number of hypotheses are simultaneously tested.
Common methods for adjustment
Suppose that there are m hypotheses of H1, …, Hm being simultaneously tested, which correspond to the initially computed P values of p1, …, pm. Accordingly, the adjusted P values of multiple comparisons are denoted as p′1, …, p′m. The pre-specified and adjusted significance levels are further denoted as α and α’, respectively. Furthermore, we assume that all hypotheses are ordered as H(1), …, H(m) according to their observed P values of p(1)≤...≤p(m); and the associated P values and significance level are denoted as p(i), p′(i) and α′(i) for the ith ordered hypothesis of H(i). We here provide an illustrative example for demonstrating differences among various adjustment methods. Let m=6 and α=0.05; and the initially computed P values corresponding to six hypotheses are p1=0.1025, p2=0.0085, p3=0.0045, p4=0.0658, p5=0.0201 and p6=0.0304, respectively.
Bonferroni adjustment
Bonferroni adjustment is one of the most commonly used approaches for multiple comparisons (5). This method tries to control FWER in a very stringent criterion and compute the adjusted P values by directly multiplying the number of simultaneously tested hypotheses (m):

Equivalently, we could let the observed P values unchanging and directly adjust the significance level as α′ = α/m = 0.05/6. For our illustrative example the adjusted P values are compared with the pre-specified significance level α=0.05, and the statistical conclusion is obviously altered before and after adjustment (Figure 2). Bonferroni adjustment has been well acknowledged to be much conservative especially when there are a large number of hypotheses being simultaneously tested and/or hypotheses are highly correlated.
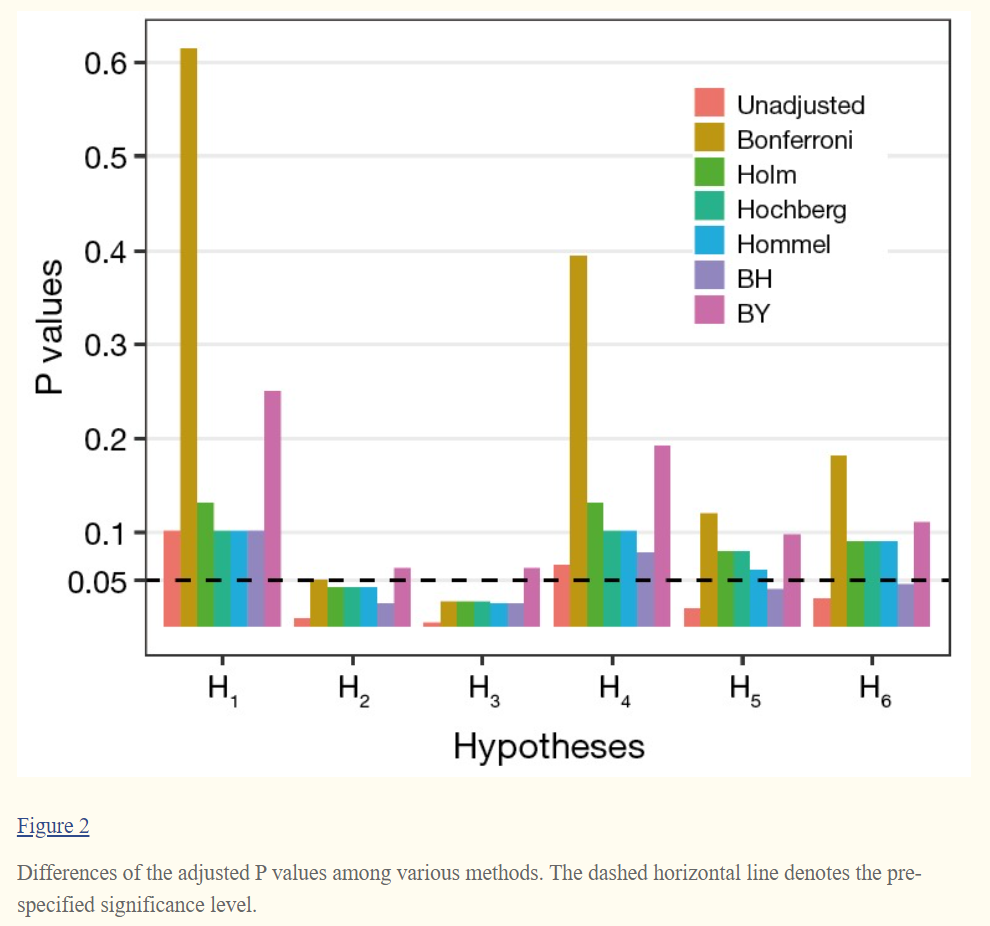
Holm adjustment
On the basis of Bonferroni method, Holm adjustment was subsequently proposed with less conservative character (6). Holm method, in a stepwise way, computes the significance levels depending on the P value based rank of hypotheses. For the ith ordered hypothesis H(i), the specifically adjusted significance level is computed:

The observed P value p(i) of hypothesis H(i) is then compared with its corresponding α′(i) for statistical inference; and each hypothesis will be tested in order from the smallest to largest P values (H(1), …, H(m)). The comparison will immediately stop when the first p(i) ≥ α′(i) is observed (i=1, ..., m) and hence all remaining hypotheses of H(j) (j=i,…,m) are directly declared non-significant without requiring individual comparison (Figure 3). Alternatively, it could directly compute the adjusted P value for each hypothesis and produce same conclusion (Figure 2).

Hochberg adjustment
Similar to Holm method, Hochberg adjustment employs same formula for computing the associated significance levels (7). Therefore, the specifically adjusted significance level for ith ordered hypothesis H(i) is also computed:
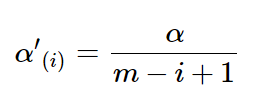
However, Hochberg method conducts statistical inference of hypothesis by starting with the largest P value (H(m), …, H(1)). When we first observe p(i) < α′(i) for hypothesis H(i) (i=m,…,1), the comparison stops and then concludes that the hypotheses of H(j) (j=i,…,1) will be rejected at significance level α. The adjusted P values of Hochberg method are shown in Figure 2. It is also known that Hochberg adjustment is more powerful than Holm method.
Hommel adjustment
Simes (1986) modified Bonferroni method and proposed a global test of m hypotheses (8). Let H={ H(1), …, H(m)} be the global intersection hypothesis, H will be rejected if p(i) ≤ iα/m for any i=1, …, m. However, Simes global test could not be used for assessing the individual hypothesis Hi. Therefore, Hommel (1988) extended Simes’ method for testing individual Hi (9). Let an index of j=max{i∈{1, ..., m}:p(m−i+k)>kα/i for k=1, ..., i} be the size of the largest subset of m hypotheses for which Simes test is not significant. All Hi (i=1,…,m) are rejected if j does not exist, otherwise reject all Hi with pi≤α/j. Although straightforward explanation for computing the adjusted P values of Hommel method would be not easy, this task could be conveniently performed by computer tools, such as the p.adjust() function in R stats package (http://cran.r-project.org).
Benjamini-Hochberg (BH) adjustment
In contrast to the strong control of FWER, Benjamini and Hochberg [1995] introduced a method for controlling FDR, which is herein termed BH adjustment (10). Let be the pre-specified upper bound of FDR (e.g., q=0.05), the first step is to compute index:

If k does not exist, reject no hypothesis, otherwise reject hypothesis of Hi (i=1,…,k). BH method starts with comparing H(i) from the largest to smallest P value (i=m,…,1). The FDR-based control is less stringent with the increased gain in power (Figure 2) and has been widely used in cases where a large number of hypotheses are simultaneously tested.
Benjamini and Yekutieli (BY) adjustment
Similar to BH method, a more conservative adjustment was further proposed for controlling FDR by Benjamini and Yekutieli [2001], and this method is also termed BY adjustment (11). Let again q be the pre-specified upper bound of FDR, the index k is computed as:
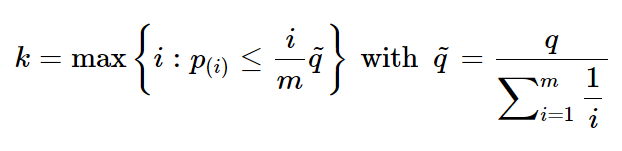
If does not exist, reject no hypothesis, otherwise reject hypothesis of Hi (i=1,…,k). BY method could address the dependency of hypotheses with increased advantages.
Conclusions
Although substantial literature has been published for addressing the increased Type I errors of multiple comparisons during the past decades, many researchers are puzzling in selecting an appropriate adjustment method. Therefore, it would be helpful for providing a straightforward overview on the adjustment for multiple comparisons to researchers who don’t have good background in statistics. Of course, there are many theoretical topics and methodological issues having not been addressed yet in the present paper, such as resampling-based adjustment methods, choice of significance level α, and specific concerns for genomics data. It is also beyond the scope of this paper to discuss the sophisticated mathematical issues in this filed.
J Grad Med Educ. 2021 Aug;13(4):457-460.
doi: 10.4300/JGME-D-21-00599.1. Epub 2021 Aug 13.
Facts and Fictions About Handling Multiple Comparisons
Gail M Sullivan 1, Richard S Feinn 2
Affiliations collapse
Affiliations
- 1is Editor-in-Chief, Journal of Graduate Medical Education (JGME), and Associate Director for Education, Center on Aging, and Professor of Medicine, University of Connecticut Health Center.
- 2is Statistical Editor, JGME, and Associate Professor of Medical Sciences, Quinnipiac University.
- PMID: 34434505
- PMCID: PMC8370375 (available on 2022-08-01)
- DOI: 10.4300/JGME-D-21-00599.1
'Articles (Medical Education) > 의학교육연구(Research)' 카테고리의 다른 글
| When I say … 리커트 문항(Med Educ, 2021) (0) | 2021.11.02 |
|---|---|
| 정답은 하나? (성찰적) 주제분석의 옳바른 실천은 무엇인가? (Qualitative Research in Psychology, 2021) (0) | 2021.10.22 |
| 통계학개론 (Adv Health Sci Educ Theory Pract. 2019) (0) | 2021.10.22 |
| 모두에게 맞는 사이즈는 없다: 보건전문직교육 연구에서 개인-중심 분석(Perspect Med Educ, 2020) (0) | 2021.08.27 |
| 이론을 명시적으로 만들기: 의학교육 연구자는 이론과의 연계성을 어떻게 기술하는가(BMC Med Educ, 2017) (0) | 2021.08.25 |